Search

» » Coherent interfaces govern direct transformation from graphite to diamond - Nature.com

Coherent interfaces govern direct transformation from graphite to diamond - Nature.com

susilangs.blogspot.com

Abstract

Understanding the direct transformation from graphite to diamond has been a long-standing challenge with great scientific and practical importance. Previously proposed transformation mechanisms1,2,3, based on traditional experimental observations that lacked atomistic resolution, cannot account for the complex nanostructures occurring at graphite−diamond interfaces during the transformation4,5. Here we report the identification of coherent graphite−diamond interfaces, which consist of four basic structural motifs, in partially transformed graphite samples recovered from static compression, using high-angle annular dark-field scanning transmission electron microscopy. These observations provide insight into possible pathways of the transformation. Theoretical calculations confirm that transformation through these coherent interfaces is energetically favoured compared with those through other paths previously proposed1,2,3. The graphite-to-diamond transformation is governed by the formation of nanoscale coherent interfaces (diamond nucleation), which, under static compression, advance to consume the remaining graphite (diamond growth). These results may also shed light on transformation mechanisms of other carbon materials and boron nitride under different synthetic conditions.

Main

Carbon has numerous allotropes owing to its ability to form various bonds through orbital hybridization. Among all the allotropes, graphite and diamond (with sp2 and sp3 hybridization, respectively) are the most ubiquitous and have been extensively exploited by humans for several millennia. Although both occur in nature, the synthesis of diamond from graphite was not successful until the middle of the last century6,7. The transformation from graphite to diamond can be made under different synthetic conditions, such as high pressure, high temperature (HPHT) with6 or without7,8 a catalyst, explosive shock9, and low-temperature compression under severe shear deformation10. Along with these experimental efforts, understanding the transformation from graphite to diamond has attracted broad attention but remained a significant challenge11.

Largely based on diffraction data from recovered samples, several concerted transformation mechanisms were proposed to account for the graphite-to-diamond transformation1,2. In hexagonal graphite (HG), graphene layers are arranged in AB-type stacking, with carbon atoms in each layer bonded covalently in a honeycomb-like lattice through sp2 hybridization. According to the concerted transformation mechanisms, HG undergoes several possible variations in stacking order to transform into cubic diamond (CD) or hexagonal diamond (HD) where all carbon atoms are bonded covalently by sp3 hybridization. The AB stacking may change into ABC stacking, followed by collective puckering to transform into CD2. Alternatively, the AB stacking may change either to AA stacking followed by puckering to transform into HD1, or to AB′ stacking followed by puckering to transform into CD or buckling to transform into HD2. Some reports, again largely based on diffraction data, have suggested that formation of HD is energetically favoured at lower synthesis temperatures12. This prompted nucleation-and-growth models3,13 with two types of transient heterophase junction proposed between diamond nuclei and the graphite matrix11,14: one is a graphite–diamond diphase connected with weak van der Waals interaction, and the other is covalently bonded interfaces between diamond and graphitic domains with a reduced interlayer distance of less than 2.5 Å. Similar to the nucleation-and-growth mechanisms, a wave-like lattice buckling and slipping model suggested a stacking-order change from AB to ABC by bending graphitic layers, followed by formation of transient heterophase junctions to complete the transformation to CD15.

Despite the numerous mechanisms proposed, the graphite-to-diamond transformation process remains elusive. The main obstacle to understanding the transformation is that the process occurs under HPHT without in situ information, particularly at the atomic scale. Post-mortem examinations on the structure of products recovered from HPHT-treated graphite typically rely on X-ray diffraction (XRD), which is insensitive to small amounts of defects or intermediate phases in the sample. In the absence of microscopic information, interpretation of the XRD data is sometimes non-unique, thus leading to different conclusions12,16,17. More recently, high-resolution transmission electron microscopy (HRTEM) has been applied to natural and laboratory-shocked samples4,5, and has revealed two types of diamond–graphene composite nanostructure, which are named as type 1 and type 2 diaphite structures following the original definition of diaphite18. In type 1 diaphite, a few graphene layers are inserted parallelly within {111} diamond; in type 2 diaphite, graphitic layers are inserted at high angles within {113} diamond4,5. The proposed crystal structure gives rise to diffraction peaks resembling those of graphite (with an interlayer spacing of 3.0 Å) and CD. Although the origin of this hybrid structure and its correlation with the graphite-to-diamond transformation remains unclear4,5, the idea of a hybrid structure provides an alternative view of the reported ‘compressed graphite’ with a 3.1-Å interlayer spacing12,19,20,21,22,23, and may play an important role in understanding the graphite-to-diamond transformation.

In this study, we investigate the products from graphite treated under static HPHT conditions with state-of-the-art scanning transmission electron microscopy (STEM). Partially transformed samples are characterized by graphite and diamond nanodomains interlocked via coherent interfaces. The graphite domains, with interlayer spacings centring at about 3.1 Å, are intimately connected to diamond domains with numerous stacking faults. Atomic-resolution high-angle annular dark-field (HAADF) STEM observations reveal four basic structural motifs constituting the graphite–diamond interfaces. Theoretical calculations suggest a progressive graphite-to-diamond transformation process characterized by formation of graphite–diamond interfaces and subsequent advance of the interfaces for diamond growth, consistent with the atomically resolved interface structures as well as interface propagation observed by in situ STEM. This work thus clarifies the long-standing puzzle since the first successful static synthesis of diamond.

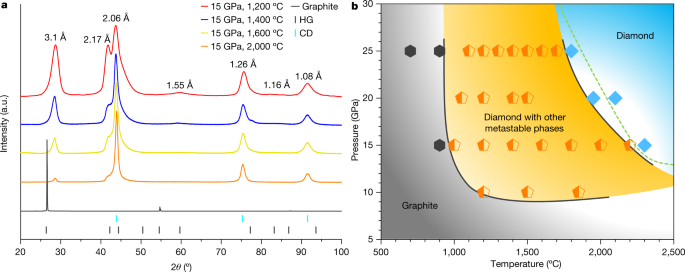
Selected XRD patterns of partially transformed samples recovered from 15 GPa and temperatures between 1,200 °C and 2,000 °C are shown in Fig. 1a, along with the pristine graphite whose strong and sharp (00l) peak indicates excellent crystallinity. After HPHT treatment, the main diffraction peaks are consistent with those previously observed in graphite compressed at moderate temperatures12, where peaks not belonging to CD were attributed to the so-called compressed graphite (3.1 Å and 1.55 Å) and HD (2.17 Å and 1.16 Å). Such assignments, however, are under debate12,24. With increasing synthesis temperature and under identical heating duration, intensities of diffraction peaks from CD increase, whereas the other peaks gradually diminish. A kinetic phase diagram is constructed based on XRD measurements, as shown in Fig. 1b. Graphite remains unchanged in low-temperature (T < 900 °C) and low-pressure (P < 10 GPa) regions. Above 900 °C and 10 GPa, a multiphase region emerges (orange field), where CD co-exists with other metastable carbon phases such as compressed graphite. At sufficiently high temperatures and pressures, the recovered samples are predominantly CD (light blue field). The well established equilibrium phase boundary between graphite and diamond is drawn as the dashed line25.

Fig. 1: XRD patterns and phase evolution diagram of graphite under HPHT.
figure 1

a, XRD of samples recovered from 15 GPa and 1,200 °C, 1,400 °C, 1,600 °C and 2,000 °C. The pristine graphite is included for comparison. The coloured tags at the bottom indicate standard diffraction lines of graphite (HG) and cubic diamond (CD). b, Kinetic phase diagram of graphite under HPHT determined from the XRD results. Hexagons, pentagons and diamond symbols represent samples that are pure graphite, mixed phases containing CD and other metastable carbon phases, and pure diamond, respectively. Collectively, these data points define three regions as delineated by the solid lines. The dashed line is the established phase boundary between graphite and diamond.

Full size image

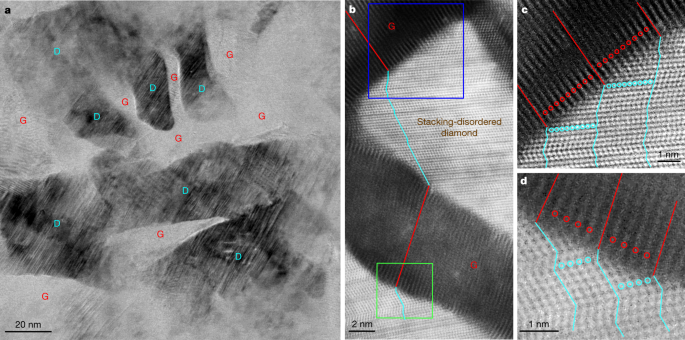
Detailed TEM observations on quenched samples provide direct insight into the mechanism of graphite-to-diamond transformation under static compression. Extended Data Fig. 1a–d shows typical microstructures of samples recovered from 15 GPa and various temperatures. All recovered samples are composed of diamond and (compressed) graphite, and the fraction of the graphitic phase decreases with increasing synthesis temperature, which is consistent with the results from XRD and Rietveld refinement analysis (Fig. 1a and Extended Data Fig. 1e–i). Figure 2a is a bright-field (BF)-STEM image from a sample recovered from 15 GPa and 1,200 °C, in which diamond (D) and graphite (G) nanodomains are clearly distinguished. In neighbouring diamond and graphite domains, the lattice fringes of the two phases are tilted relative to one another, forming interfaces different from the (113)CD or (111)CD types as previously proposed for meteoritic or laboratory-shocked diamonds based on TEM observations4,5,11,14,26. High-resolution HAADF-STEM observations further confirm the tightly bonded graphitic and diamond domains (Fig. 2b). The graphite domains show a reduced interlayer spacing of about 3.1 Å, and the lattice fringes are distorted, especially adjacent to the interfaces. The diamond domains exhibit considerable stacking disorder in the close-packed carbon bilayers. Magnified HAADF-STEM images in Fig. 2c,d reveal a remarkable one-to-one correspondence between atomic layers in graphite and kinked carbon bilayers in diamond. Hereafter, this unique hybrid carbon, which consists of nanoscale graphite and diamond units bonding each other through coherent interfaces, is referred to as Gradia. The corresponding interface is referred to as the gradia interface. The phase/microstructure evolution of graphite under different pressure–temperature conditions (Fig. 1b and Extended Data Fig. 1) and the observed gradia interfaces suggest that the formation and migration of the interfaces play a decisive role in graphite-to-diamond transformation under static pressure: diamond growth is accomplished by advancing the interfaces into graphite.

Fig. 2: Microstructures of a sample recovered from 15 GPa and 1,200 °C.
figure 2

a, Low-magnification BF-STEM image showing nanoscaled diamond (D) domains embedded in graphite (G). b, High-resolution HAADF-STEM image of graphite domains showing a reduced interlayer spacing of 3.1 Å and diamond domains with numerous stacking faults, with well defined interfaces between the two phases. Alternating red and cyan lines delineate the end-to-end connectivity between one atomic layer in graphite and kinked carbon bilayer in diamond traversing multiple graphite and diamond domains. c, d, Magnified HAADF-STEM images corresponding to the blue-boxed (c) and green-boxed (d) regions in b. The red and cyan lines and circles highlight the one-to-one correspondence between the atomic layers in graphite and the kinked carbon bilayers in diamond, respectively.

Full size image

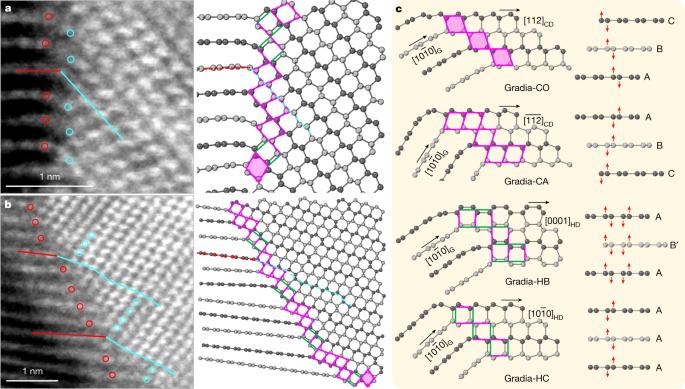
Examples of HAADF-STEM images of gradia interfaces are shown in Fig. 3 and Extended Data Fig. 2. The graphite and diamond domains exhibit the following orientation relations: [1\(\bar{2}\)10]G//[1\(\bar{1}\)0]CD or [1\(\bar{2}\)10]HD, with no definitive epitaxial relationship across the interface. On the basis of the HAADF-STEM observations, four primary structural motifs are identified to constitute the gradia interfaces, as shown in Fig. 3c where the corresponding puckering and buckling processes in graphitic layers with different stacking orders are indicated by red arrows. When viewed along [1\(\bar{1}\)0]CD, the (111)CD and (11\(\bar{1}\))CD planes form a rhombic pattern with equal side lengths of 2.18 Å. A rhombus in CD can connect to the (0001) lattice of compressed graphite through a vertex with either an obtuse or an acute angle, forming two structural motifs, which are referred to as Gradia-CO and Gradia-CA, respectively. Similarly, when viewed along [1\(\bar{2}\)10]HD, the (10\(\bar{1}\)0)HD and (0002)HD planes form a rectangular pattern with two side lengths of 2.18 Å and 2.06 Å, respectively. The adjacent (0001) layers of compressed graphite can either buckle into a boat conformation and transform into (10\(\bar{1}\)0)HD with a d-spacing (the distance between planes of atoms that give rise to the diffraction peaks) of 2.18 Å, or pucker into a chair conformation and transform into (0002)HD with a d-spacing of 2.06 Å. These two structural motifs are referred to as Gradia-HB and Gradia-HC, respectively.

Fig. 3: Coherent interface structures between graphite and diamond.
figure 3

a, b, Atomic-resolution HAADF-STEM images of two gradia interfaces (left) and the corresponding atomic models (right). The red and cyan lines (circles) delineate the one-to-one correspondence between graphite and diamond. In the atomic models, adjacent graphitic layers are coloured with different greyscales for clarity. Structural motifs at the interface are denoted with rhombi (with or without shadows) and rectangles (with different orientations). c, Four representative gradia interfaces. The pink and green sides in patterns indicate side lengths of 2.18 Å and 2.06 Å, respectively. See main text for details of nomenclature.

Full size image

Under HPHT, atomic layers in graphite endure compression, bending and interlayer sliding, resulting in highly localized variations in interlayer distance, curvature and stacking order, which may induce new bonding across neighbouring graphite layers to form different interface structures. The gradia interface made up of the aforementioned structural motifs has great variability and flexibility to accommodate such local structural variations (Fig. 3c). It is noted that although both Gradia-HB and Gradia-HC can co-exist with Gradia-CO and Gradia-CA, Gradia-HB and Gradia-HC are mutually exclusive (Fig. 3 and Extended Data Fig. 2). This is because a plane cannot be completely filled by two differently oriented rectangles, with all vertices overlapping. Under HPHT conditions, gradia interfaces advance into graphite, promoting diamond growth. For example, Extended Data Fig. 3a,b shows schematically the advance of the Gradia-CO and Gradia-HC interfaces (Fig. 3c) into graphite, with several new motifs forming at the frontline. Similar growth processes also occur for other gradia interfaces with different combinations of structural motifs. As the interface advances to the graphite side, the specifically combined structural motifs impose constraints on the bonding of carbon atoms in adjacent graphite layers, resulting in significant stacking disorder of carbon bilayers in the as-grown diamond (Fig. 3 and Extended Data Fig. 2). The absence of a definitive epitaxial relationship across the gradia interface is also determined by such transformation processes. Instead, varying tilting angles between graphite and diamond layers across the interface as well as varying interlayer spacing between graphite layers are shown (Extended Data Fig. 2). Our Gradia structures are clearly different from previously proposed structures, such as type 2 diaphite4,5,27, and the interstratified graphite and diamond26, where definitive topotactic relationships were observed between graphite and diamond (Extended Data Fig. 4). It may be worth noting that the STEM observations did not identify any pure HD domains in the recovered samples, even though the XRD patterns show a prominent peak at 2.17 Å and two weaker ones at 1.93 Å (shoulder) and 1.16 Å, which were previously attributed to HD12. Actually, all diamond domains are characterized by a high density of stacking faults. Similar hexagonal-cubic stacking disorders also exist in natural and laboratory-shocked diamonds24, and account for the hexagonal feature in diffraction patterns16,17. One thus should exercise caution when claiming new diamond phases. This potential ambiguity does not preclude the existence of HD though. For example, we did observe an HD nanodomain, 3 nm in thickness and 30 nm laterally from HPHT-treated carbon onions28. Larger HD phases may be produced with carefully selected carbon precursors and fine-tuned pressure–temperature conditions.

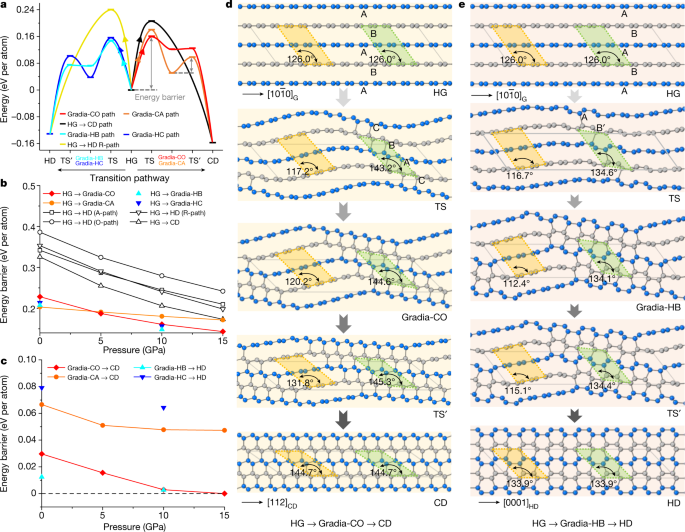
To understand the origin of gradia interfaces and their roles in graphite-to-diamond transformation, we conducted first-principles calculations on intentionally designed hybrid crystals with the characteristic gradia interfaces shown in Fig. 3c (see Methods, Extended Data Figs. 5–7 and Extended Data Table 1 for more details). As shown in Extended Data Fig. 5, the unit cell for each hypothetic crystal is separated into sp2-hybridized graphitic (grey-coloured atoms) and sp3-hybridized diamond (gold-coloured atoms) sections that are bonded coherently through a gradia interface (green-coloured atoms). The thermodynamic, mechanical and dynamic stabilities of these crystal structures are shown in Extended Data Fig. 7. Transformation energy barriers from graphite to diamond through these intermediate crystal structures were evaluated under pressure with the variable-cell nudged-elastic-band (VCNEB) simulation method29,30 as implemented in the USPEX code31,32. The transformation processes are summarized in Fig. 4 and Extended Data Fig. 8. The energy barriers required to form gradia interfaces directly from graphite are all higher than those for diamond growth by advancing the gradia interfaces into graphite (Fig. 4a). It is noted that in all considered cases, the energy barriers decrease monotonically with increasing pressure in the range of 0–15 GPa (Fig. 4b,c), and the transformation barriers along the pathways through the gradia interfaces are substantially lower than those along classic concerted transformation pathways29. Moreover, the calculated transformation barrier from graphite to Gradia structures would decrease with increasing unit cell size or graphite fraction (Extended Data Fig. 8a,b).

Fig. 4: Energy barriers and transformation process from graphite to diamond through intermediate crystals (hypothetic) containing gradia interfaces.
figure 4

a, Energy profile of graphite-to-diamond transformation through different pathways at 10 GPa. The maximum energy barrier occurs when the wavy graphitic layers start bonding, that is, forming the gradia interface along HG to intermediate crystal. TS represents the transition states of the pathway from graphite to intermediate crystal; TS’ represents the transition states of the pathway from intermediate crystal to diamond. b, Energy barriers decrease with increasing pressure from HG to intermediate crystal. The classic concerted transformation pathways previously proposed—that is, HG→CD and HG→HD (A-path, R-path, O-path)—are from ref. 29. c, Energy barriers decrease with increasing pressure from intermediate crystal to CD (or HD). The energy barrier in this stage (diamond growth) is significantly lower than that in the nucleation stage (gradia interface formation). Above 10 GPa, Gradia-CO and Gradia-HB crystals can convert into diamond with almost no energy barrier. d,e, The structure snapshots during graphite-to-diamond transformation through Gradia-CO (d) and Gradia-HB crystals (e) at 10 GPa. The adjacent graphitic layers are distinguished with grey and blue colours. Under pressure, the graphite layers bend wavily. Bonding across graphite layers starts in the green-shadowed regions with a reduced interlayer spacing of about 2.1 Å, whereas the interlayer spacing increases from 2.9 Å to 3.2 Å in the yellow-shadowed regions, leaving graphite stable. Next, the interfaces advance gradually into graphite, and diamond nuclei eventually grow into pure diamond. The angles in the green- and yellow-shadowed regions indicate the localized changes in the structure.

Full size image

Figure 4d,e and Extended Data Fig. 8c,d provide atomistic snapshots from pure graphite to diamond under 10 GPa through hypothetic crystals with different gradia interfaces (see Supplementary Videos 1–4 for the whole processes). During the transformation, graphite layers undergo wave-like bending with remarkable localized variations in stacking order and interlayer spacing, inducing additional bonding across adjacent graphite layers to form gradia interfaces in regions with suitable stacking order and interlayer spacing. For example, Fig. 4d shows five snapshots of the transformation from HG to CD. The oscillation of the graphitic layers (second snapshot from the top) results in localized changes of stacking order from AB to CBA accompanied by reduced interlayer spacing, leading to the formation of a Gradia-CO interface and the appearance of the first diamond-like bonding. At this diamond nucleation stage, the energy barrier reaches the maximum (Fig. 4a). The gradia interface then advances from both sides into graphitic sections, resulting in the growth of diamond lattice (third and fourth snapshots) until the transformation to CD is complete (fifth snapshot). In contrast, the previously proposed wave-like buckling and slipping mechanism invokes uniform interlayer distances without forming gradia interfaces15. Figure 4a suggests that once a gradia interface is formed, further formation of diamond is energetically favoured even under metastable conditions. This is confirmed by in situ STEM observations (Extended Data Fig. 3c,d). Under electron-beam irradiation in vacuum, new diamond-like atomic bonding is identified from the graphite side of the Gradia-CO interface. This remarkable observation is due to the lower energy barrier for diamond growth through step-by-step advancing of the gradia interface.

By integrating sp2-hybridized graphite and sp3-hybridized diamond nanodomains with strong coherent interfaces, Gradia has the prospect of combining the advantages of both parties, with potentially a wide range of properties for multifunctional applications4. The gradia interfaces may also play a substantial role in tuning material properties. For example, the calculation results suggest that the designed hybrid crystals display obvious metallicity (Extended Data Figs. 5 and 6), contributed mostly by atoms in the graphitic section and gradia interface. It is noted that the contribution to the metallicity from interface atoms is comparable to, or even higher than, that from graphitic atoms in Gradia-CO and Gradia-HB crystals, owing to the presence of sp2-hybridized atoms (circled in red) at the interface. In Gradia, the proportion-tunable graphite and diamond domains together with the versatile gradia interfaces offer additional freedom in engineering nanostructures, for desired properties. Specifically, differently hybridized carbon atoms in Gradia contribute to different functionalities, for example, sp3 atoms to superhardness, sp2 atoms to electrical conductivity, and sp2–sp3 mixed atoms near the interfaces to toughness4. With regulated fractions and distributions of different types of atom, a variety of properties, which are inaccessible for diamond and graphite separately, may be tailored for Gradia (Extended Data Fig. 9).

The transformation from graphite to diamond under static compression occurs in two stages, that is, the formation of a coherent gradia interface (diamond nucleation) and subsequently the advance of the interface (diamond growth). The transformation mechanism clarified in this work can serve as guidance in understanding the transformations of boron nitride and other carbon phases such as carbon nanotubes and onions under high pressure. Beyond the transformation mechanism, the observed Gradia marks a major step towards nanostructure and properties engineering in diamond-related materials, and provides opportunities in pursuing desired combination of mechanical and electronic properties, such as simultaneous superhardness, high toughness and electrical conductivity.

Methods

Sample synthesis

The Gradia-containing samples were synthesized from graphite (99.99%, Alfa Aesar) under conditions of 10–25 GPa and 1,000–2,300 °C. HPHT experiments were performed with a 10-MN double-stage large-volume multi-anvil system by using standard COMPRES 10/5 (or 8/3) sample assembly consisting of a 10-mm (or 8-mm) spinel + magnesium oxide octahedron with a rhenium heater and a LaCrO3 thermal insulator. Temperature was measured with type-C tungsten–rhenium thermocouples, and pressure was estimated from previously determined calibration curves. During the synthesis, pressure increased at 2 GPa per hour to the target pressure; then the sample was heated at a rate of 20 °C per minute to the target temperature. In all the experiments, the sample was maintained under the target pressure and temperature for 2 h. After that, the sample was cooled to room temperature at 50 °C per minute, followed by pressure release at a rate of 2 GPa per hour. Back-transformation of diamond during pressure release at room temperature is unlikely, considering that graphitization of diamond occurs only at high temperature. The recovered sample rods were 1–2.5 mm in diameter and height.

Ultra-thin TEM sample preparation

To eliminate grain overlaps in STEM imaging, foils with a thickness of about 60 nm were cut with a focus ion beam (FEI Helios 5 CX DualBeam), and further thinned to 20 nm with low-energy argon-ion milling (Fischione Model 1040 NanoMill). Before loading into the microscope, the foils were cleaned with H2/O2 plasma (Gatan 695 Plasma cleaner) for 40 s to eliminate possible carbon contamination.

HAADF-STEM measurement

STEM measurements were conducted with a spherical aberration-corrected scanning transmission electron microscope (FEI Themis Z), with a monochromator, operating at an accelerating voltage of 300 kV. The electron-beam damage to the STEM specimen was consciously avoided or minimized in the STEM observations. In low-magnification BF-STEM mode, the electron irradiation dose is relatively low, which cannot cause noticeable damage to the sample. For high-resolution STEM observations, a very low beam current of 50 pA was used to reduce irradiation damage, with a short dwelling time of 0.2 μs. BF, low-angle ADF (LAADF) and HAADF images were obtained by combining 20 frames from acquired series with drift correction (DCFI in software of Velox, Thermo Fisher). No obvious change in the interface structure was found by comparing these frames, indicating that electron irradiation damage on the interface structure is negligible. The probe convergence angle was set at 25 mrad. The collecting angles of BF and LAADF were set at 6 mrad and 16−62 mrad, respectively. The collecting angle of HAADF was set at 65−200 mrad to eliminate effects of coherent scattering.

X-ray diffraction

Powder X-ray diffraction patterns of recovered samples were collected using Bruker D8 Discover (Cu Kα).

Mechanical property measurement

A microhardness tester (KB 5 BVZ) was used to measure Vickers hardness HV and fracture toughness KIc of samples by using a diamond Vickers indenter, and to measure Knoop hardness HK with a diamond Knoop indenter. HV was determined from HV = 1,854.4P/d12, where d1 (µm) is the arithmetic mean of the two diagonals of Vickers indentation. HK was determined from HK = 14,229P/d22, where P (N) is the applied load and d2 (µm) is the major diagonal length (long axis) of rhomboid-shaped Knoop indentation. The adopted loading and dwelling times were 40 s and 20 s, respectively. Five hardness data points were obtained at each load, and the hardness values were determined from the asymptotic-hardness region. KIc was calculated from KIc = 0.016(E/HV)0.5F/C1.5 for radial cracks formed on surfaces of bulk samples, where F (in N) is the applied load, C (in µm) is the average length of the radial cracks measured from the indent centre, and E is Young’s modulus, which is 1,140 GPa for diamond.

Electrical resistivity measurement

The electrical resistivities of samples were measured in the range of 4–300 K by using the van der Pauw method in the Physical Property Measurement System (PPMS, Quantum Design). The effects of electrodes on the resistivity measurements can be avoided through transforming the current direction in different van der Pauw probes. Four electrodes were taped onto insulating quartz plates (5 × 5 mm in size) and placed onto the sample for conductivity measurements. The sample surfaces were first polished with diamond submicrometre powder before measurement.

Density-functional-theory simulation

The hypothetic crystal structures based on gradia interfaces were constructed with the Materials Visualizer module in Materials Studio (Accelrys Software). The calculations were performed on the basis of density functional theory as implemented in the CASTEP code33, and the ultrasoft pseudopotentials were used34,35. The local density approximation exchange-correlation functional of Ceperley and Alder parameterized by Perdew and Zunger (CA–PZ) was utilized for structural optimization and calculations of total energies, band structures, elastic properties and phonon spectra36,37. A k-point sampling38 of 2π × 0.03 Å−1 and a plane-wave cut-off of 600 eV were used. Band structures were also calculated with Perdew−Burke−Ernzerhof (PBE) and Heyd–Scuseria–Ernzerhof (HSE06) functionals as implemented in the Vienna ab initio simulation package (VASP)39 to illustrate the reliability of the band structure calculations (Extended Data Fig. 6). The selected calculation parameters were all tested to ensure that energy convergence was less than 1 meV per atom. For comparison, we also performed similar calculations on pure graphite and diamond crystals. To reveal the transformation mechanism from graphite to diamond through the gradia interfaces, we performed VCNEB simulations29,30 at 0 GPa, 5 GPa, 10 GPa and 15 GPa, as implemented in the USPEX code31,32. Both initial and final states were relaxed at set pressures. Then, the initial pathways were subsequently refined by the VCNEB method and optimized to find the minimum-energy pathways. The forces and stresses were computed by VASP code39 with the local density approximation exchange-correlation functional of CA–PZ36,37. The projector augmented-wave method was adopted, with 2s22p2 treated as valence electrons for the C atom. Plane-wave cut-off energies were 600 eV and k-point meshes were sampled with the resolution of 2π × 0.04 Å−1. Spring constants were set as 40 eV Å−2. The climbing image technique40 was used to precisely locate transition states after hundreds of VCNEB steps. For the mechanical stability, the 13 independent elastic constants Cij for a stable monoclinic structure should satisfy the Born stability criteria41,42,43,44.

Data availability

The data that support the findings of this study are available from the corresponding author upon request.

References

  1. Fahy, S., Louie, S. G. & Cohen, M. L. Theoretical total-energy study of the transformation of graphite into hexagonal diamond. Phys. Rev. B 35, 7623–7626 (1987).

    ADS  CAS  Article  Google Scholar 

  2. Scandolo, S., Bernasconi, M., Chiarotti, G. L., Focher, P. & Tosatti, E. Pressure-induced transformation path of graphite to diamond. Phys. Rev. Lett. 74, 4015–4018 (1995).

    ADS  CAS  PubMed  Article  Google Scholar 

  3. Khaliullin, R. Z., Eshet, H., Kühne, T. D., Behler, J. & Parrinello, M. Nucleation mechanism for the direct graphite-to-diamond phase transition. Nat. Mater. 10, 693–697 (2011).

    ADS  CAS  PubMed  Article  Google Scholar 

  4. Németh, P. et al. Complex nanostructures in diamond. Nat. Mater. 19, 1126–1131 (2020).

    ADS  PubMed  Article  CAS  Google Scholar 

  5. Németh, P. et al. Diamond-graphene composite nanostructures. Nano Lett. 20, 3611–3619 (2020).

    ADS  PubMed  PubMed Central  Article  CAS  Google Scholar 

  6. Bundy, F. P., Hall, H. T., Strong, H. M. & Wentorf, R. H. Man-made diamonds. Nature 176, 51–55 (1955).

    ADS  CAS  Article  Google Scholar 

  7. Bundy, F. P. Direct conversion of graphite to diamond in static pressure apparatus. Science 137, 1057–1058 (1962).

    ADS  CAS  PubMed  Article  Google Scholar 

  8. Irifune, T., Kurio, A., Sakamoto, S., Inoue, T. & Sumiya, H. Ultrahard polycrystalline diamond from graphite. Nature 421, 599–600 (2003).

    ADS  CAS  PubMed  Article  Google Scholar 

  9. DeCarli, P. S. & Jamieson, J. C. Formation of diamond by explosive shock. Science 133, 1821–1822 (1961).

    ADS  CAS  PubMed  Article  Google Scholar 

  10. Dong, J. et al. Decompression-induced diamond formation from graphite sheared under pressure. Phys. Rev. Lett. 124, 065701 (2020).

    ADS  CAS  PubMed  Article  Google Scholar 

  11. Zhu, S.-C., Yan, X.-Z., Liu, J., Oganov, A. R. & Zhu, Q. A revisited mechanism of the graphite-to-diamond transition at high temperature. Matter 3, 864–878 (2020).

    Article  Google Scholar 

  12. Bundy, F. P. & Kasper, J. S. Hexagonal diamond—a new form of carbon. J. Chem. Phys. 46, 3437–3446 (1967).

    ADS  CAS  Article  Google Scholar 

  13. Britun, V. F., Kurdyumov, A. V. & Petrusha, I. A. Diffusionless nucleation of lonsdaleite and diamond in hexagonal graphite under static compression. Powder Metall. Met. Ceram. 43, 87–93 (2004).

    CAS  Article  Google Scholar 

  14. Xie, Y.-P., Zhang, X.-J. & Liu, Z.-P. Graphite to diamond: origin for kinetics selectivity. J. Am. Chem. Soc. 139, 2545–2548 (2017).

    CAS  PubMed  Article  Google Scholar 

  15. Xie, H., Yin, F., Yu, T., Wang, J.-T. & Liang, C. Mechanism for direct graphite-to-diamond phase transition. Sci. Rep. 4, 5930 (2015).

    Article  CAS  Google Scholar 

  16. Salzmann, C. G., Murray, B. J. & Shephard, J. J. Extent of stacking disorder in diamond. Diam. Relat. Mater. 59, 69–72 (2015).

    ADS  CAS  Article  Google Scholar 

  17. Murri, M. et al. Quantifying hexagonal stacking in diamond. Sci. Rep. 9, 10334 (2019).

    ADS  PubMed  PubMed Central  Article  CAS  Google Scholar 

  18. Ohnishi, H. & Nasu, K. Photoinduced domain-type collective structural changes with interlayer σ-bonds in the visible region of graphite. Phys. Rev. B 79, 054111 (2009).

    ADS  Article  CAS  Google Scholar 

  19. Álvarez-Murga, M. et al. “Compressed graphite” formed during C60 to diamond transformation as revealed by scattering computed tomography. Phys. Rev. Lett. 109, 025502 (2012).

    ADS  PubMed  Article  CAS  Google Scholar 

  20. Hu, M. et al. Compressed glassy carbon: an ultrastrong and elastic interpenetrating graphene network. Sci. Adv. 3, e1603213 (2017).

    ADS  PubMed  PubMed Central  Article  CAS  Google Scholar 

  21. Irifune, T. et al. Formation of pure polycrystalline diamond by direct conversion of graphite at high pressure and high temperature. Phys. Earth Planet. Inter. 143–144, 593–600 (2004).

    ADS  Article  CAS  Google Scholar 

  22. Niwase, K. et al. Quenchable compressed graphite synthesized from neutron-irradiated highly oriented pyrolytic graphite in high pressure treatment at 1500 °C. J. Appl. Phys. 123, 161577 (2018).

    ADS  Article  CAS  Google Scholar 

  23. Yang, X. et al. Diamond–graphite nanocomposite synthesized from multi-walled carbon nanotubes fibers. Carbon 172, 138–143 (2021).

    CAS  Article  Google Scholar 

  24. Németh, P. et al. Lonsdaleite is faulted and twinned cubic diamond and does not exist as a discrete material. Nat. Commun. 5, 5447 (2014).

    ADS  PubMed  Article  CAS  Google Scholar 

  25. Bundy, F. P. et al. The pressure–temperature phase and transformation diagram for carbon; updated through 1994. Carbon 34, 141–153 (1996).

    CAS  Article  Google Scholar 

  26. Garvie, L. A. J., Nemeth, P. & Buseck, P. R. Transformation of graphite to diamond via a topotactic mechanism. Am. Mineral. 99, 531–538 (2014).

    ADS  Article  Google Scholar 

  27. Németh, P. et al. Diaphite-structured nanodiamonds with six- and twelve-fold symmetries. Diam. Relat. Mater. 119, 108573 (2021).

    ADS  Article  CAS  Google Scholar 

  28. Yue, Y. et al. Hierarchically structured diamond composite with exceptional toughness. Nature 582, 370–374 (2020).

    ADS  CAS  PubMed  Article  Google Scholar 

  29. Dong, X. et al. An ab initio study on the transition paths from graphite to diamond under pressure. J. Phys. Condens. Matter 25, 145402 (2013).

    ADS  PubMed  Article  CAS  Google Scholar 

  30. Qian, G.-R. et al. Variable cell nudged elastic band method for studying solid–solid structural phase transitions. Comput. Phys. Commun. 184, 2111–2118 (2013).

    ADS  CAS  Article  Google Scholar 

  31. Glass, C. W., Oganov, A. R. & Hansen, N. USPEX—evolutionary crystal structure prediction. Comput. Phys. Commun. 175, 713–720 (2006).

    ADS  CAS  MATH  Article  Google Scholar 

  32. Lyakhov, A. O., Oganov, A. R., Stokes, H. T. & Zhu, Q. New developments in evolutionary structure prediction algorithm USPEX. Comput. Phys. Commun. 184, 1172–1182 (2013).

    ADS  CAS  Article  Google Scholar 

  33. Clark, S. J. et al. First principles methods using CASTEP. Z. Krist. Cryst. Mater. 220, 567–570 (2005).

    CAS  Article  Google Scholar 

  34. Laasonen, K., Car, R., Lee, C. & Vanderbilt, D. Implementation of ultrasoft pseudopotentials in ab initio molecular dynamics. Phys. Rev. B 43, 6796–6799 (1991).

    ADS  CAS  Article  Google Scholar 

  35. Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 41, 7892–7895 (1990).

    ADS  CAS  Article  Google Scholar 

  36. Perdew, J. P. & Zunger, A. Self-interaction correction to density-functional approximations for many-body systems. Phys. Rev. B 23, 5048–5079 (1981).

    ADS  CAS  Article  Google Scholar 

  37. Ceperley, D. M. & Alder, B. J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett. 45, 566–569 (1980).

    ADS  CAS  Article  Google Scholar 

  38. Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).

    ADS  MathSciNet  Article  Google Scholar 

  39. Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).

    ADS  CAS  Article  Google Scholar 

  40. Henkelman, G., Uberuaga, B. P. & Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 113, 9901–9904 (2000).

    ADS  CAS  Article  Google Scholar 

  41. Mouhat, F. & Coudert, F.-X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 90, 224104 (2014).

    ADS  Article  CAS  Google Scholar 

  42. Born, M., Huang, K. & Lax, M. Dynamical theory of crystal lattices. Am. J. Phys. 23, 474–474 (1955).

    ADS  Article  Google Scholar 

  43. Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. A 65, 349–354 (1952).

    ADS  Article  Google Scholar 

  44. Born, M. On the stability of crystal lattices. I. Math. Proc. Camb. Phil. Soc. 36, 160–172 (1940).

    ADS  MathSciNet  CAS  MATH  Article  Google Scholar 

  45. Ohnishi, H. & Nasu, K. Generation and growth of sp3-bonded domains by visible photon irradiation of graphite. Phys. Rev. B 80, 014112 (2009).

    ADS  Article  CAS  Google Scholar 

  46. Radosinski, L., Formalik, F., Olejniczak, A. & Radosz, A. Diaphite, a new type of surface with mixed sp2–sp3 hybridization for adsorption and functionalization. Appl. Surf. Sci. 404, 154–161 (2017).

    ADS  CAS  Article  Google Scholar 

  47. Luo, K. et al. Design of a class of new sp2–sp3 carbons constructed by graphite and diamond building blocks. Chin. Phys. Lett. 38, 028102 (2021).

    ADS  CAS  Article  Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (numbers 52090020, 91963203, 51772260, U20A20238, 12174200, 52025026, 52073245, 51722209, 51525205 and 52103322), and the National Key R&D Program of China (2018YFA0703400 and 2018YFA0305900). Z.Z. acknowledges the NSF for Distinguished Young Scholars of Hebei Province of China (E2018203349). The calculations were performed and supported by Tianhe II in Guangzhou and Supercomputing Center of Nankai University (NKSC).

Author information

Author notes

  1. These authors contributed equally: Kun Luo, Bing Liu, Wentao Hu, Xiao Dong

Authors and Affiliations

  1. Center for High Pressure Science (CHiPS), State Key Laboratory of Metastable Materials Science and Technology, Yanshan University, Qinhuangdao, China

    Kun Luo, Bing Liu, Wentao Hu, Yufei Gao, Lei Sun, Zhisheng Zhao, Yingju Wu, Yang Zhang, Mengdong Ma, Xiang-Feng Zhou, Julong He, Dongli Yu, Zhongyuan Liu, Bo Xu & Yongjun Tian

  2. Key Laboratory for Microstructural Material Physics of Hebei Province, School of Science, Yanshan University, Qinhuangdao, China

    Kun Luo, Yingju Wu & Yang Zhang

  3. School of Physics and MOE Key Laboratory of Weak-Light Nonlinear Photonics, Nankai University, Tianjin, China

    Xiao Dong

  4. Center for Advanced Radiation Sources, The University of Chicago, Chicago, IL, USA

    Yanbin Wang

  5. School of Materials and Chemical Engineering, Zhongyuan University of Technology, Zhengzhou, China

    Quan Huang

Authors
  1. Kun Luo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bing Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wentao Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xiao Dong
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Yanbin Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Quan Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Yufei Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Lei Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Zhisheng Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Yingju Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Yang Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  12. Mengdong Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  13. Xiang-Feng Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  14. Julong He
    View author publications

    You can also search for this author in PubMed Google Scholar

  15. Dongli Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  16. Zhongyuan Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  17. Bo Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  18. Yongjun Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Z.Z., B.X. and Y.T. conceived this project. K.L., B.L., D.Y. and Z.Z. prepared the samples. K.L., B.L., Y.Wu and M.M. measured XRD. W.H., K.L. and L.S. conducted TEM characterization. K.L., Z.Z. and B.X. determined the Gradia structures. K.L., Q.H. and J.H. performed the structural stability calculations. X.D. and X.-F.Z. performed the transition pathway calculations. K.L., B.L. and Y.G. measured mechanical property and electrical resistivity. K.L., Z.Z., B.X., Y.Wang, Y.T., Z.L. and Y.Z. analysed the data. K.L., Z.Z., B.X., Y.Wang and Y.T. drafted the manuscript with contributions from all authors. K.L., B.L., W.H. and X.D. contributed equally to this work.

Corresponding author

Correspondence to Zhisheng Zhao.

Ethics declarations

Competing interests

Z.Z., K.L., B.L., W.H., L.S., J.H., D.Y., Y.T., B.X. and Z.L. are inventors on patent applications related to this work filed by Yanshan University (CN110330006A, filed 5 August 2019; US20210039950A1, filed 6 March 2020; EP3772486A1, filed 6 March 2020; JP2021024774A, filed 14 April 2020). The other authors declare no competing interests.

Peer review

Peer review information

Nature thanks Yingxiang Cai, Peter Nemeth and Alfonso San Miguel for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data figures and tables

Extended Data Fig. 1 Typical microstructures and Rietveld refinement analysis of samples recovered from 15 GPa and various temperatures.

a, 1,200 °C. b, 1,400 °C. c, 1,600 °C. d, 2,000 °C. With increasing synthesis temperature, the graphitic regions (enclosed with red curves) in the recovered samples decreases gradually. All scale bars are 20 nm. e−h, Rietveld refinement for different samples. Black bars: 'compressed graphite'; cyan bars: HD; orange bars: CD. i, Mass fraction of graphitic component in the samples with increasing synthesis temperature.

Extended Data Fig. 2 Atomic-resolution HAADF-STEM images of various gradia interfaces.

a–f, The average interlayer distances in graphite regions are 3.13 Å (a), 3.11 Å (b), 3.20 Å (c), 3.02 Å (d), 2.93 Å (e), and 3.09 Å (f). Red and cyan lines/circles indicate the one-to-one coherence between the atomic layers in graphite and the kinked carbon bilayers in diamond. Different stacking modes in diamond regions are emphasized with rhombi and rectangles (CD and HD motifs), respectively. All scale bars are 0.5 nm.

Extended Data Fig. 3 The advance of gradia interfaces into graphite.

a, Several new Gradia-CO motifs (open red rhombi) advancing into graphite one step further from initial Gradia-CO interface (filled magenta rhombi) shown in Fig. 3c. b, Several new Gradia-HC motifs (open red rectangles) advancing into graphite one or more steps further from initial Gradia-HC interface (filled cyan rectangles) shown in Fig. 3c. c, d, The interface propagation with extra bonding under electron-beam irradiation during STEM observation. The LAADF-STEM images captured at the same area illustrate atomic bonding at the interface. The white dotted circles mark the C−C dumbbell units in diamond, and the red ones correspond to the newly formed C−C units in diamond at the interface. All scale bars are 0.5 nm.

Extended Data Fig. 4 Comparison of different carbon structures.

a, The originally defined diaphite, that is, a bilayer structure with one third of atoms (coloured in red) forming bonds between layers, which is referred to as '2D diaphite' hereafter, has neither graphite unit nor diamond unit in the structure (adapted with permission from ref. 45, Fig. 5c. Copyright 2009 by the American Physical Society). b, The originally defined 2D diaphite structure used for surface adsorption propertie calculation, yellow carbon atoms indicate extruded sites for hydrogen adsorption (adapted with permission from ref. 46, Fig. 1. Copyright 2017 by Elsevier B.V.). c, Model structures for type 1 and type 2 diaphite. For type 2 diaphite, graphite and diamond regions are also connected via bonded interfaces, but without a one-to-one correspondence: depending on the choice of diamond {111} planes, 4 graphene layers are corresponding to 6 or 3 diamond (111) planes (see the interface in the red dashed circle in c) (adapted from ref. 5, Fig. 3a and 3b. CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/)). d, Four structural models for Gradia-CO, Gradia-CA47, Gradia-HB, and Gradia-HC with fully coherent interfaces, that is a one-to-one correspondence in atomic positions between graphite and diamond layers across the interface. They show different tilting angles between graphite and diamond layers and different interlayer spacings in graphitic regions. These newly found structures are clearly different from the 2D diaphite45, type 1, and type 2 diaphite5.

Extended Data Fig. 5 Hypothetical crystal structures with characteristic gradia interfaces and the corresponding electronic structures.

a, Gradia-CO. b, Gradia-CA. c, Gradia-HB. d, Gradia-HC. The hypothetical crystals are named after the gradia interfaces shown in Fig. 3c. For each of the crystal models displayed, the thickness of the cell perpendicular to the page is the lattice constant of graphite [010]HG (or [110]CD and [010]HD). Details of structural information are listed in Extended Data Table 1. In each crystal structure, the grey-line grid indicates the unit cell employed for transformation energy barrier calculation, the cyan-shadowed area indicates the primitive cell. Carbon atoms are differently coloured: grey for sp2-hybridized atoms in graphitic sections, gold for sp3-hybridized atoms in diamond-structured sections, and green for those in gradia interfaces (among the interface atoms, atoms circled in red are sp2-hybridized, the others are sp3-hybridized). The lower part of each panel shows the calculated electronic structure with the bands across the Fermi level coloured in blue. In each DOS graph, the partial DOS (in unit of states per eV per atom) from interface, graphitic and diamond-structured atoms are coloured in green (int.), grey (gra.) and gold (dia.), respectively. Substantial contributions from the interface atoms to the density of states (DOS) near the Fermi level are revealed, especially for Gradia-CO and Gradia-HB crystals (a and c) with sp2-hybridized atoms at the interface. For instance, the electronic structure and partial density of states (PDOS) of Gradia-CO demonstrates a clear metallicity because of several electron bands across the Fermi level. The electronic states around Fermi level mainly come from the px and pz orbitals from two sets of carbon atoms: C1 atoms (sp2-hybridized ones at the interface, red-circled) and C2 atoms (at the zigzag edge of graphene layer connecting the interface).

Extended Data Fig. 6 The ambient-pressure band structures of four Gradia structures calculated by DFT-PBE and HSE06 functional as implemented in VASP code.

There are bands across the Fermi level, indicating metallic Gradia-CO, Gradia-CA, Gradia-HB, and semimetallic Gradia-HC at ambient pressure.

Extended Data Fig. 7 Thermodynamic, mechanical, and dynamic stabilities of four crystal structures shown in Extended Data Figure 5.

a, Formation enthalpies with respect to graphite as a function of applied pressure. Crystals containing gradia interfaces become stable energetically relative to graphite at high pressures in the range of 10−20 GPa. Note that Gradia-CO and Gradia-HB transform directly into CD and HD above 11 GPa and 19 GPa, respectively. This might be related to the high-energy sp2-hybridized atoms at gradia interfaces, which can contribute to diamond growth by advancing the interface towards the graphite side under pressure. b, Calculated elastic constants (Cij, GPa), bulk moduli (B, GPa), shear moduli (G, GPa), and Young's moduli (E, GPa) of hypothetical crystal structures at ambient pressure. Clearly, the calculated elastic constants Cij of crystal structures satisfy the mechanical stability criteria, confirming their mechanical stability at ambient pressure. c, Calculated phonon spectra of the hypothetical crystal structures at ambient pressure. No imaginary phonon frequencies throughout the whole Brillouin zone indicates that all the structures are dynamically stable.

Extended Data Fig. 8 Transformation process from graphite to diamond through Gradia crystals.

a, Energy profile of transformation from graphite to Gradia-CO structures with different unit cell size or different graphite and diamond fractions at 10 GPa. b, Nomenclature of Gradia-CO (m, n): m is the number of six-numbered rings to be formed between adjacent layers in graphite domain, and n is the number of six-numbered rings formed in diamond domain. Red dotted lines indicate further bonding to six-numbered rings for a complete transformed diamond. c, d, Structure snapshots during graphite-to-diamond transformation through Gradia-CA and Gradia-HC crystals, respectively, at 10 GPa.

Extended Data Fig. 9 Mechanical and electrical properties of Gradia samples.

a, Knoop hardness (HK) as a function of applied loads for Gradia samples quenched from 15 GPa/1,200 °C (black), 15 GPa/1,600 °C (turquoise), and 15 GPa/2,000 °C (red). Error bars represent one s.d. (n = 5). HK of three samples under 9.8 N load are 51 ± 4.7, 69 ± 6.0, and 115 ± 9.3 GPa, respectively. In comparison, HK of binderless nanopolycrystalline diamond (NPD) under 9.8 N is 111 ± 15.2 GPa. b, A photograph of black Gradia sample with a polished surface (15 GPa/2,000 °C). c, Vickers indentation fracture toughness of Gradia (15 GPa/2,000 °C), binderless nanopolycrystalline diamond (NPD) and single-crystal diamond (SC-D, (111) face). The estimation of fracture toughness of materials is based on the length of cracks generated on the sample with a Vickers indenter of square-pyramid diamond under high loads of 49 N (for Gradia and NPD) and 19.6 N (for SC-D). All scale bars are 20 µm. Unlike other materials with obvious cracks, no visible crack was generated in Gradia, indicating an excellent toughness of Gradia. The fracture toughness is 8.7 ± 1.8 MPa·m0.5 for NPD and 6.4 ± 1.1 MPa·m0.5 for SC-D. d, Temperature-dependent electrical resistivities of Gradia samples, showing a semiconducting characteristic. With increasing synthesis temperature, the diamond content in Gradia increases gradually, resulting in an increase in electrical resistivity. Gradia samples recovered from 15 GPa/1,200 °C and 15 GPa/1,600 °C show low resistivities, while the sample recovered from 15 GPa/2,000 °C shows a significantly high resistivity. The mechanical and electrical properties of Gradia can be tunable by adjusting the proportions of graphite and diamond in the bulk.

Extended Data Table 1 Space group (S.G.), lattice parameters (L.P., Å) and atomic Wyckoff positions of the hypothetical Gradia crystal structures shown in Extended Data Fig. 5 at ambient pressure
Full size table

Supplementary information

Supplementary Video 1

Transformation process from graphite to cubic diamond through Gradia-CO at 10 GPa. The detailed analysis is shown in Fig. 4.

Supplementary Video 2

Transformation process from graphite to cubic diamond through Gradia-CA at 10 GPa. The detailed analysis is shown in Fig. 4 and Extended Data Fig. 8c.

Supplementary Video 3

Transformation process from graphite to hexagonal diamond through Gradia-HB at 10 GPa. The detailed analysis is shown in Fig. 4.

Supplementary Video 4

Transformation process from graphite to hexagonal diamond through Gradia-HC at 10 GPa. The detailed analysis is shown in Fig. 4 and Extended Data Fig. 8d.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Luo, K., Liu, B., Hu, W. et al. Coherent interfaces govern direct transformation from graphite to diamond. Nature (2022). https://ift.tt/sThYnci

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://ift.tt/sThYnci

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Adblock test (Why?)



"direct" - Google News
July 06, 2022 at 11:58PM
https://ift.tt/pMYWlg7

Coherent interfaces govern direct transformation from graphite to diamond - Nature.com
"direct" - Google News
https://ift.tt/gKuI7JD
https://ift.tt/Qz6iI27
Direct

Bagikan Berita Ini

0 Response to "Coherent interfaces govern direct transformation from graphite to diamond - Nature.com"

Post a Comment

Subscribe to: Post Comments (Atom)
Powered by Blogger.